Informed Search Algorithms in AI

In this page, we will learn about Informed Search Algorithms in AI, Pure Heuristic Search, Best first Search Algorithm (Greedy Search), A* Search Algorithm, and Algorithm of A* search.

So far we have talked about the uninformed search algorithms which looked through search space for all possible solutions of the problem without having any additional knowledge about search space. However, an educated search algorithm includes information such as how far we are from the objective, the cost of the trip, and how to get to the destination node. This knowledge allows agents to explore less of the search area and discover the goal node more quickly.

For huge search spaces, the informed search algorithm is more useful. Because the informed search algorithm is based on the concept of heuristics, it is also known as heuristic search.

Heuristics function: A heuristic is a function that finds the most promising path in Informed Search. It takes the agent's current state as input and outputs an estimate of how near the agent is to the goal. The heuristic method, on the other hand, may not always provide the optimum solution, but it guarantees that a good solution will be found in a fair amount of time. A heuristic function determines how close a state is to the desired outcome. It calculates the cost of an ideal path between two states and is represented by h(n). The heuristic function's value is always positive.

h(n) <= h*(n)

Here h(n) is heuristic cost, and h*(n) is the estimated cost. Hence heuristic cost should be less than or equal to the estimated cost.

Pure Heuristic Search:

The simplest type of heuristic search algorithm is pure heuristic search. It grows nodes according to their heuristic value h. (n). It has two lists: an OPEN list and a CLOSED list. It places nodes that have previously expanded in the CLOSED list, and nodes that have not yet been expanded in the OPEN list.

Each iteration, the lowest heuristic value node n is extended, and all of its successors are generated, and n is added to the closed list. The algorithm keeps running until a goal state is discovered.

We shall cover two main algorithms in the informed search, which are listed below:

  • Best First Search Algorithm(Greedy search)
  • A* Search Algorithm

1.) Best-first Search Algorithm (Greedy Search):

The greedy best-first search algorithm always chooses the path that appears to be the most appealing at the time. It's the result of combining depth-first and breadth-first search algorithms. It makes use of the heuristic function as well as search. We can combine the benefits of both methods with best-first search. At each step, we can use best-first search to select the most promising node. We expand the node that is closest to the goal node in the best first search method, and the closest cost is determined using a heuristic function, i.e.

f(n)= g(n).

Were, h(n)= estimated cost from node n to the goal.

The priority queue implements the greedy best first algorithm.

Best first search algorithm:

Step 1: Place the initial node in the OPEN list first.

Step 2: Stop and return failure if the OPEN list is empty.

Step 3: Move the node n from the OPEN list to the CLOSED list, as it has the lowest value of h(n).

Step 4: Extend node n and construct node n's descendants.

Step 5: Examine each successor of node n to see whether any of them is a goal node. Return success and end the search if any successor node is a goal node; otherwise, proceed to Step 6.

Step 6: The method checks for the evaluation function f(n) for each successor node, then determines if the node has been in the OPEN or CLOSED list. Add the node to the OPEN l if it isn't already on both lists.

Step 7: return to the step 2

Advantages:

  • By combining the benefits of both algorithms, best first search may switch between BFS and DFS.
  • This algorithm outperforms the BFS and DFS algorithms in terms of efficiency.

Disadvantages:

  • In the worst-case scenario, it can act like an unguided depth-first search.
  • As with DFS, it's possible to get stuck in a loop.
  • This algorithm isn't optimal.

Example:

Consider the search problem below, which we'll solve with greedy best-first search. Each node is extended at each iteration using the evaluation function f(n)=h(n), as shown in the table below:

informed search algorithms

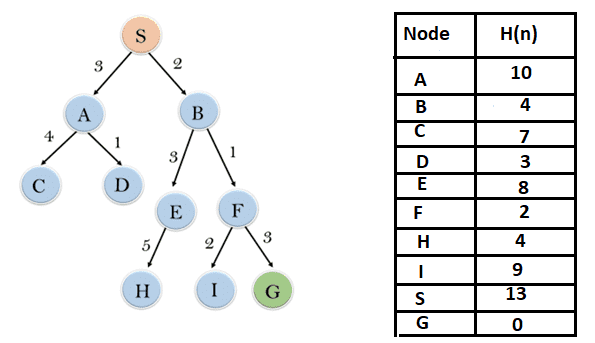
In this search example, we are using two lists which are OPEN and CLOSED Lists. Following are the iteration for traversing the above example.

informed search algorithms 2

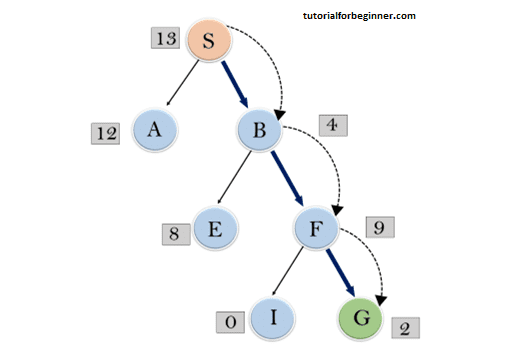
Expand the nodes of S and put in the CLOSED list

Initialization: Open [A, B], Closed [S]

Iteration 1: Open [A], Closed [S, B]

Iteration 2: Open [E, F, A], Closed [S, B]
: Open [E, A], Closed [S, B, F]

Iteration 3: Open [I, G, E, A], Closed [S, B, F]
: Open [I, E, A], Closed [S, B, F, G]

Therefore, the final solution path will be: S----> B----->F----> G

Time Complexity: The Greedy best first search's worst case time complexity is O(bm).

Space Complexity: The Greedy best first search's worst case space complexity is O(bm). Where m is the search space's maximum depth.

Complete: Even if the given state space is finite, greedy best-first search is still imperfect.

Optimal: The greedy best-first-search algorithm isn't optimal.

2.) A* Search Algorithm:

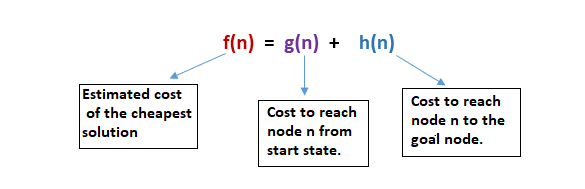
The most well-known type of best-first search is the A* search. It employs the heuristic function h(n) and the cost of getting from state g to node n. (n). It solves the problem efficiently by combining UCS and greedy best-first search features. Using the heuristic function, the A* search algorithm finds the shortest path through the search space. This search algorithm uses a smaller search tree and delivers the best results faster. The A* method is similar to UCS, but instead of g(n)+h(n), it uses g(n)+h(n) (n).

We employ a search heuristic as well as the cost to reach the node in the A* search algorithm. As a result, we can add both expenses together as follows, and this total is referred to as a fitness number.

informed search algorithms 3

Note: Only the nodes with the lowest value of f(n) are extended at each point in the search space, and the procedure ends when the goal node is located.

Algorithm of A* search:

Step 1: Place the beginning node in the OPEN list as the first step.

Step 2: Determine whether or not the OPEN list is empty; if it is, return failure and stop.

Step 3: Choose the node with the shortest value of the evaluation function (g+h) from the OPEN list; if node n is the goal node, return success and stop; otherwise, return failure and continue.

Step 4: Expand node n and create all of its descendants, then place n in the closed list. Check whether n' is already in the OPEN or CLOSED list for each successor n'; if not, compute the evaluation function for n' and insert it in the Open list.

Step 5: If node n' is already in the OPEN and CLOSED states, it should be attached to the back pointer, which represents the lowest g(n') value.

Advantages:

  • When compared to other search algorithms, the A* search method is the best.
  • The A* search algorithm is ideal and comprehensive.
  • This method is capable of resolving extremely difficult issues.

Disadvantages:

  • Because it is dependent on heuristics and approximation, it does not always yield the quickest path.
  • The A* search algorithm has some concerns with complexity.
  • The fundamental disadvantage of A* is that it requires a lot of memory because it maintains all created nodes in memory, which makes it unsuitable for a variety of large-scale issues.

Example:

In this example, we'll use the A* algorithm to traverse the provided graph. We'll calculate the f(n) of each state using the formula f(n)= g(n) + h(n), where g(n) is the cost of reaching any node from the start state.

We'll use the OPEN and CLOSED lists here.

informed search algorithms 4

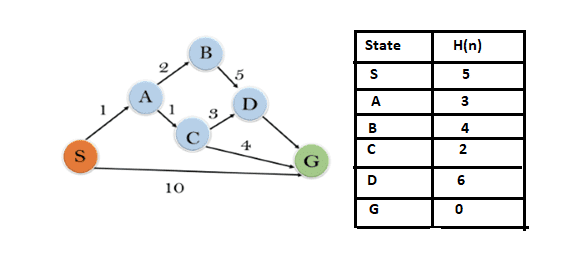
Solution:

informed search algorithms 5

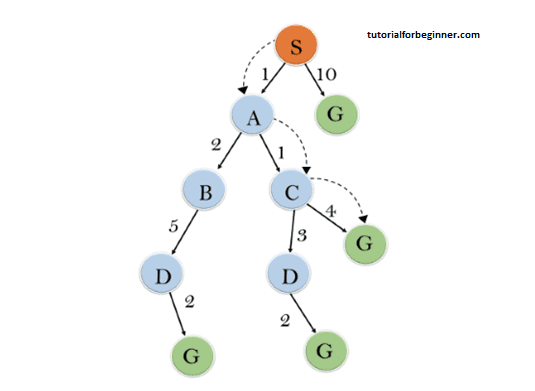
Initialization: {(S, 5)}

Initialization 1: {(S--> A, 4), (S-->G, 10)}

Initialization 2: {(S--> A-->C, 4), (S--> A-->B, 7), (S-->G, 10)}

Initialization 3: {(S--> A-->C, 4), (S--> A-->B, 7), (S-->G, 10)}

Initialization 4: will give the final result, as S--->A--->C--->G it provides the optimal path with cost 6.

Points to remember:

  • The A* algorithm returns the path that appeared initially, rather than searching for all possible paths.
  • The quality of the heuristic determines the efficiency of the A* algorithm.
  • All nodes that satisfy the criteria f are expanded by the A* algorithm (n)

Complete: The A* algorithm is complete if and only if:

  • The number of branching factors is limited.
  • Every action has a fixed cost.

Optimal: A* search method is optimal if it meets the following two criteria:

  • Admissible: The first requirement for optimality is that h(n) is an admissible A* tree search heuristic. An acceptable heuristic is one that is optimistic.
  • Consistency: It is the second necessary requirement for only A* graph-search.

A* tree search will always identify the least expensive path if the heuristic function is accepted.

Time Complexity: The A* search algorithm's time complexity is determined by the heuristic function, and the number of nodes expanded is proportional to the depth of the solution d. So, where b is the branching factor, the temporal complexity is O(b^d).

Space Complexity: The A* search algorithm has an O(b^d) space complexity.